Courses M2 : CR16 - Data analysis and processing for networks
Pierre BORGNAT -- pierre.borgnat@ens-lyon.fr
Jean-Christophe PESQUET -- jean-christophe.pesquet@u-pem.fr
Nelly PUSTELNIK -- nelly.pustelnik@ens-lyon.fr
These lectures will cover modern techniques in signal processing for data which are distributed over networks.
Analysis of data over networks or graphs (also called graph signals) is currently a very active research domain, and we will study approaches combining signal and image processing, graph theory (especially algebraic methods such as spectral analysis of graphs), and distributed methods on networks.
The application of signal processing for networks ranges from the study of technological networks (of sensors, in telecommunication or transport) to more general complex networks such as biological or social networks.
Three main topics will be explored.
First, harmonic analysis on graphs will be discussed, going from simple Fourier transform suited to graph signals to multi-scale wavelet analysis.
Second, variational approaches on graphs will be discussed, allowing to design methods such as denoising, restoration, inference or clustering on graphs.
For this purpose, modern optimization approaches based on monotone operators will also be introduced.
Finally, distributed methods will be considered, especially for consensus, estimation or detection in a network, including methods using distributed optimization.
Examples :
-
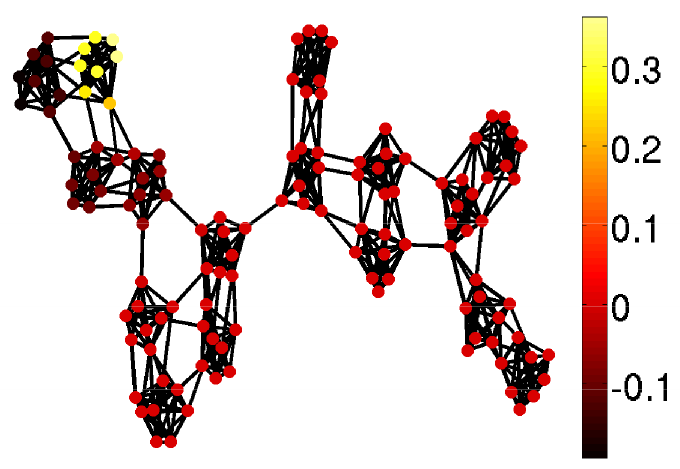
Mode decomposition on graphs
(Source: http://perso.ens-lyon.fr/nicolas.tremblay/) -
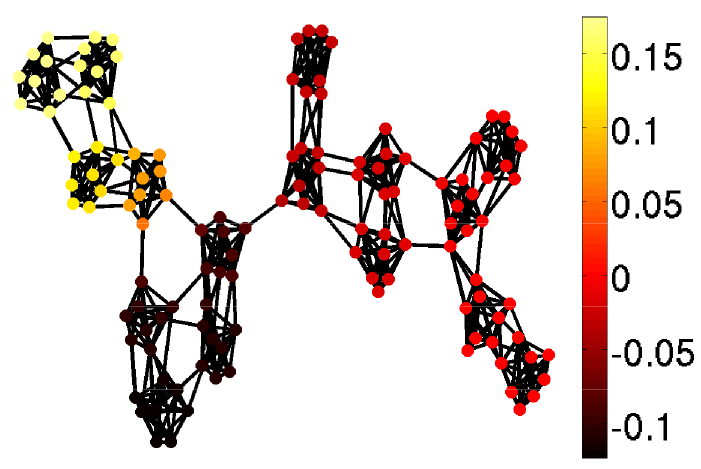
Multi-scale wavelet analysis for graph
(See: http://lts2www.epfl.ch/) -
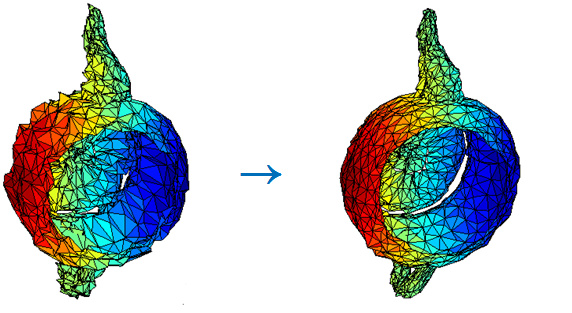
Graph denoising
(Source: http://www.esiee.fr/~coupriec/) -
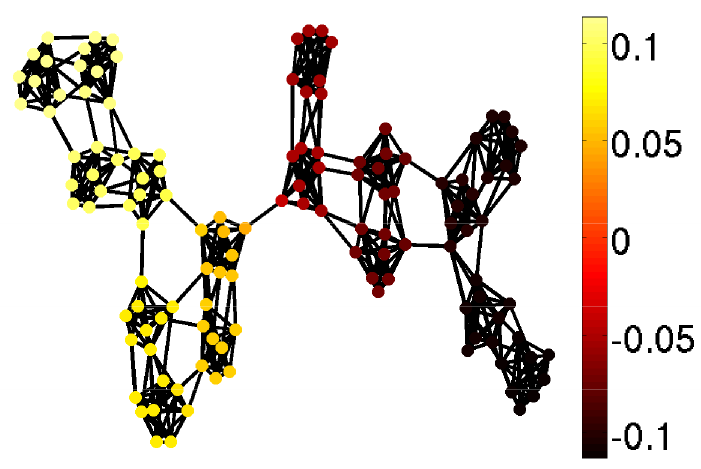
Graph clustering
(Source: http://perso.ens-lyon.fr/nicolas.tremblay//)

Slides:
- Courses 1: [Slides]
- Course 2: [Slides]
- Course 3-5: [Slides]
- Course 6: [Slides]
- Course 7: [Slides]
- Course 8: [Slides]
- Course 9: [Slides]
- Course 10: [Slides]
- TP: [Slides--Data1--Data2]
- Groupe de 2 étudiants.
- Choisir un des trois articles listés ci-dessous.
- Choix de l'article et du groupe avant le vendredi 19 décembre 2014.
- Présentation expliquant le contenu de l'article choisi (identification du problème, solution proposée par les auteurs, avis critique sur la solution retenue, liens entre le contenu de l'article et le cours).
- 10 min de présentation + 10 min de questions.
- Article 1 -- [Distributed Signal Processing via Chebyshev Polynomial Approximation]
- Article 2 -- [Estimating Traffic and Anomaly Maps via Network Tomography]
- Article 3 -- [Constrained TV-based regularization on graphs]
When and where:
- October 2014 - January 2015
- ENS Lyon, 46 allée d'Italie, 69007 Lyon